A Camera Implementation in C++

Introduction

One of the most important elements of any 3D application is its camera. A camera allows you to move around in your world and orient your view. In today’s post, I’ll put together a code walk through that will take you through a simple camera implementation.

The Concept

There are two major components of any camera. They are position and orientation. Position is fairly easy to grasp, it’s just where the camera is and is identified using a normal 3-space vector.

The more difficult of the two concepts is orientation. The best description for this that I’ve found is on the Flight Dynamics page on wikipedia. The following image has been taken from that article and it outlines the plains that orientation can occur. Of course, the image’s subject is an aircraft but the same concepts apply to a camera’s orientation:

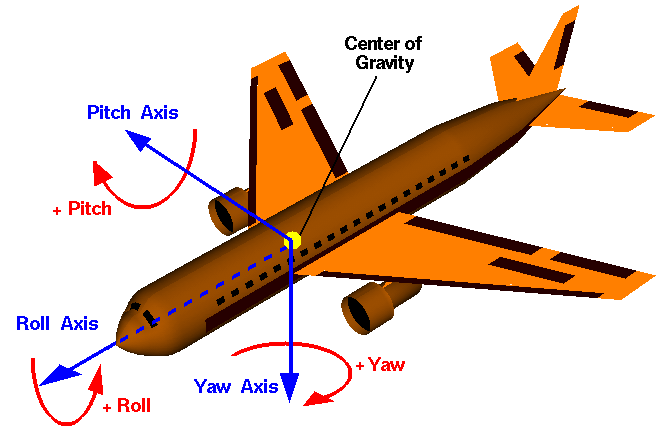
The pitch describes the orientation around the x-axis, the yaw describes the orientation around the y-axis and the roll describes the orientation around the z-axis.

With all of this information on board, the requirements of our camera should become a little clearer. We need to keep track of the following about the camera:

• Position
• Up orientation (yaw axis)
• Right direction (pitch axis)
• Forward (or view) direction (roll axis)

We’ll also keep track of how far we’ve gone around the yaw, pitch and roll axis.

Some Maths (and code)

There’s a handful of really useful equations that are going to help us out here. With all of the information that we’ll be managing and how tightly related each axis is considering they’re all relating to the same object - you can see how interactive it can be just by modifying one attribute.

When the pitch changes:

forwardVector = (forwardVector * cos(pitch)) + (upVector * sin(pitch))
upVector      = forwardVector x rightVector

void camera::pitch(const float angle) {
  // keep track of how far we've gone around the axis
  this->rotatedX += angle;

  // calculate the new forward vector
  this->viewDir = glm::normalize(
    this->viewDir * cosf(angle * PION180) +
    this->upVector * sinf(angle * PION180)
  );

  // calculate the new up vector
  this->upVector  = glm::cross(this->viewDir, this->rightVector);
  // invert so that positive goes down
  this->upVector *= -1;
}

When the yaw changes:

forwardVector = (forwardVector * cos(yaw)) - (rightVector * sin(yaw))
rightVector   = forwardVector x upVector

void camera::yaw(const float angle) {
  // keep track of how far we've gone around this axis
  this->rotatedY += angle;

  // re-calculate the new forward vector
  this->viewDir = glm::normalize(
    this->viewDir * cosf(angle * PION180) -
    this->rightVector * sinf(angle * PION180)
  );

  // re-calculate the new right vector
  this->rightVector = glm::cross(this->viewDir, this->upVector);
}

When the roll changes:

rightVector = (rightVector * cos(roll)) + (upVector * sin(roll))
upVector    = forwardVector x rightVector

void camera::roll(const float angle) {
  // keep track of how far we've gone around this axis
  this->rotatedZ += angle;

  // re-calculate the forward vector
  this->rightVector = glm::normalize(
    this->rightVector * cosf(angle * PION180) +
    this->upVector * sinf(angle * PION180)
  );

  // re-calculate the up vector
  this->upVector  = glm::cross(this->viewDir, this->rightVector);
  // invert the up vector so positive points down
  this->upVector *= -1;
}

Ok, so that’s it for orientation. Reading through the equations above, you can see that the calculation of the forward vector comes out of some standard rotations. The x operator that I’ve used above denotes vector cross product.

Now that we’re keeping track of our current viewing direction, up direction and right direction; performing camera movements is really easy.

I’ve called these advance (move along the forward plane), ascend (move along the up plane) and strafe (move along the right plane).

// z movement
void camera::advance(const float distance) {
  this->position += (this->viewDir * -distance);
}

// y movement
void camera::ascend(const float distance) {
  this->position += (this->upVector * distance);
}

// x movement
void camera::strafe(const float distance) {
  this->position += (this->rightVector * distance);
}

All we are doing here is just moving along those planes that have been defined for us via orientation. Movement is simple.

Integrating

All of this code/math is great up until we need to apply it in our environments. Most of the work that I do centralises around OpenGL, so I’ve got a very handy utility function (from GLU) that I use called gluLookAt. Plugging these values in is rather simple:

void camera::place(void) {
  glm::vec3 viewPoint = this->position + this->viewDir;

   // setup opengl with gluLookAt
  gluLookAt(
    position[0], position[1], position[2],
    viewPoint[0], viewPoint[1], viewPoint[2],
    upVector[0], upVector[1], upVector[2]
  );
}

We calculate our viewpoint as (position - forwardVector) and really just plug the literal values into this function. There is a lot of information on the gluLookAt documentation page that you can use if OpenGL isn’t your flavor to simulate what it does.

That’s it for a simple camera!